07 排列:如何让计算机学会“田忌赛马”?
你好,我是黄申。
“田忌赛马”的故事我想你肯定听过吧?田忌是齐国有名的将领,他常常和齐王赛马,可是总是败下阵来,心中非常不悦。孙膑想帮田忌一把。他把这些马分为上、中、下三等。他让田忌用自己的下等马来应战齐王的上等马,用上等马应战齐王的中等马,用中等马应战齐王的下等马。三场比赛结束后,田忌只输了第一场,赢了后面两场,最终赢得与齐王的整场比赛。
孙膑每次都从田忌的马匹中挑选出一匹,一共进行三次,排列出战的顺序。是不是感觉这个过程很熟悉?这其实就是数学中的排列过程。
我们初高中的时候,都学过排列,它的概念是这么说的:从n个不同的元素中取出m(1≤m≤n)个不同的元素,按照一定的顺序排成一列,这个过程就叫排列(Permutation)。当m=n这种特殊情况出现的时候,比如说,在田忌赛马的故事中,田忌的三匹马必须全部出战,这就是全排列(All Permutation)。
如果选择出的这m个元素可以有重复的,这样的排列就是为重复排列(Permutation with Repetition),否则就是不重复排列(Permutation without Repetition)。
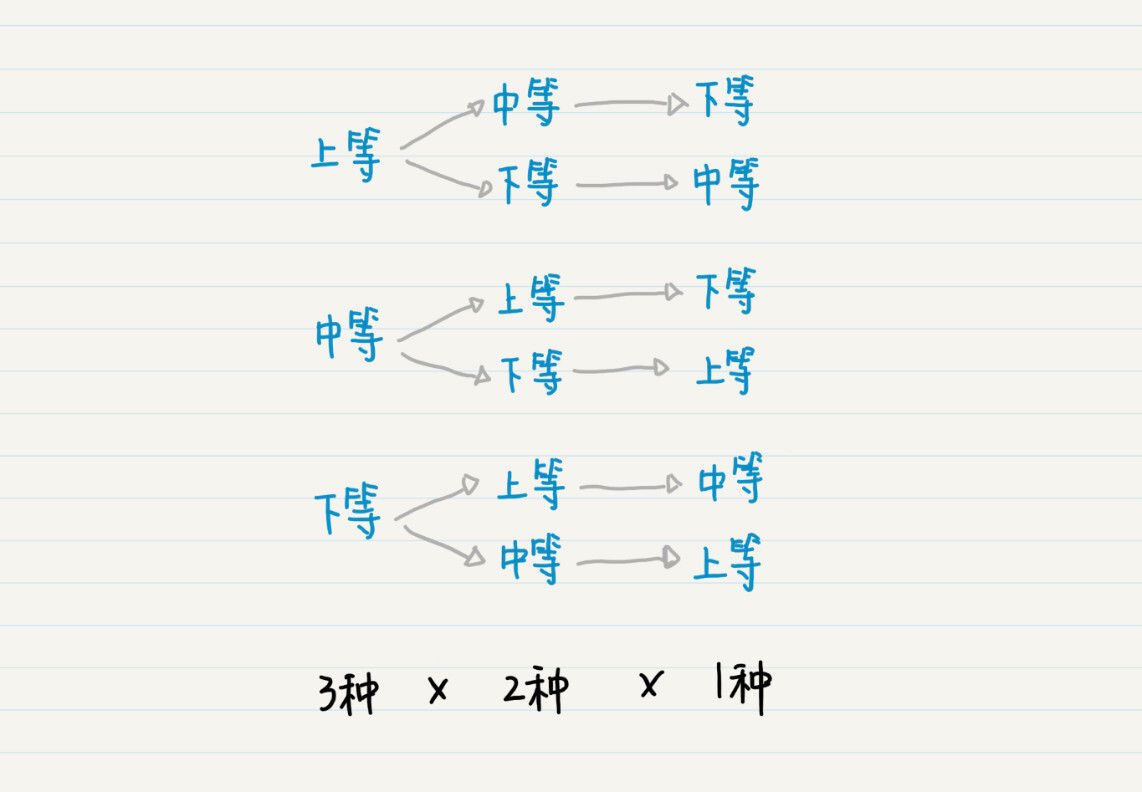
看出来没有?这其实是一个树状结构。从树的根结点到叶子结点,每种路径都是一种排列。有多少个叶子结点就有多少种全排列。从图中我们可以看出,最终叶子结点的数量是3x2x1=6,所以最终排列的数量为6。
{上等,中等,下等}
{上等,下等,中等}
{中等,上等,下等}
{中等,下等,上等}
{下等,上等,中等}
{下等,中等,上等}
我用t1,t2和t3分别表示田忌的上、中、下等马跑完全程所需的时间,用q1,q2和q3分别表示齐王的上、中、下等马跑全程所需的时间,因此,q1
如果你将这些可能的排列,仔细地和齐王的上等、中等和下等马进行对比,只有{下等,上等,中等}这一种可能战胜齐王,也就是t3>q1,t1
对于最终排列的数量,这里我再推广一下:
-
对于n个元素的全排列,所有可能的排列数量就是nx(n-1)x(n-2)x…x2x1,也就是n!;
-
对于n个元素里取出m(0≤n)个元素的不重复排列数量是nx(n-1)x(n-2)x…x(n - m + 1),也就是n!/(n-m)!。
这两点都是可以用数学归纳法证明的,有兴趣的话你可以自己尝试一下。
如何让计算机为田忌安排赛马?
我们刚才讨论了3匹马的情况,这倒还好。可是,如果有30匹马、300匹马,怎么办?30的阶乘已经是天文数字了。更糟糕的是,如果两组马之间的速度关系也是非常随机的,例如q1
如果你细心的话,就会发现在新版舍罕王赏麦的案例中,其实已经涉及了排列的思想,不过那个案例不是以“选取多少个元素”为终止条件,而是以“选取元素的总和”为终止条件。尽管这样,我们仍然可以使用递归的方式来快速地实现排列。
不过,要把田忌赛马的案例,转成计算机所能理解的内容,还需要额外下点功夫。
首先,在不同的选马阶段,我们都要保存已经有几匹马出战、它们的排列顺序、以及还剩几匹马没有选择。我使用变量result来存储到当前函数操作之前,已经出战的马匹及其排列顺序。而变量horses存储了到当前函数操作之前,还剩几匹马还没出战。变量new_result和rest_horses是分别从result和horses克隆而来,保证不会影响上一次的结果。
其次,孙膑的方法之所以奏效,是因为他看到每一等马中,田忌的马只比齐王的差一点点。如果相差太多,可能就会有不同的胜负结局。所以,在设置马匹跑完全程的时间上,我特意设置为q1
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
public class Lesson7_1 {
// 设置齐王的马跑完所需时间
public static HashMap<String, Double> q_horses_time = new HashMap<String, Double>(){
{
put("q1", 1.0);
put("q2", 2.0);
put("q3", 3.0);
}
};
// 设置田忌的马跑完所需时间
public static HashMap<String, Double> t_horses_time = new HashMap<String, Double>(){
{
put("t1", 1.5);
put("t2", 2.5);
put("t3", 3.5);
}
};
public static ArrayList<String> q_horses = new ArrayList<String>(Arrays.asList("q1", "q2", "q3"));
/**
* @Description: 使用函数的递归(嵌套)调用,找出所有可能的马匹出战顺序
* @param horses-目前还剩多少马没有出战,result-保存当前已经出战的马匹及顺序
* @return void
*/
public static void permutate(ArrayList<String> horses, ArrayList<String> result) {
// 所有马匹都已经出战,判断哪方获胜,输出结果
if (horses.size() == 0) {
System.out.println(result);
compare(result, q_horses);
System.out.println();
return;
}
for (int i = 0; i < horses.size(); i++) {
// 从剩下的未出战马匹中,选择一匹,加入结果
ArrayList<String> new_result = (ArrayList<String>)(result.clone());
new_result.add(horses.get(i));
// 将已选择的马匹从未出战的列表中移出
ArrayList<String> rest_horses = ((ArrayList<String>)horses.clone());
rest_horses.remove(i);
// 递归调用,对于剩余的马匹继续生成排列
permutate(rest_horses, new_result);
}
}
}
另外,我还使用了compare的函数来比较田忌和齐王的马匹,看哪方获胜。
public static void compare(ArrayList<String> t, ArrayList<String> q) {
int t_won_cnt = 0;
for (int i = 0; i < t.size(); i++) {
System.out.println(t_horses_time.get(t.get(i)) + " " + q_horses_time.get(q.get(i)));
if (t_horses_time.get(t.get(i)) < q_horses_time.get(q.get(i))) t_won_cnt ++;
}
if (t_won_cnt > (t.size() / 2)) System.out.println("田忌获胜!");
else System.out.println("齐王获胜!");
System.out.println();
}
下面是测试代码。当然你可以设置更多的马匹,并增加相应的马匹跑完全程的时间。
public static void main(String[] args) {
ArrayList<String> horses = new ArrayList<String>(Arrays.asList("t1", "t2", "t3"));
Lesson7_1.permutate(horses, new ArrayList<String>());
}
在最终的输出结果中,6种排列中只有一种情况是田忌获胜的。
[t3, t1, t2]
3.5 1.0
1.5 2.0
2.5 3.0
田忌获胜!
如果田忌不听从孙膑的建议,而是随机的安排马匹出战,那么他只有1/6的获胜概率。
说到这里,我突然产生了一个想法,如果齐王也是随机安排他的马匹出战顺序,又会是怎样的结果?如果动手来实现的话,大体思路是我们为田忌和齐王两方都生成他们马匹的全排序,然后再做交叉对比,看哪方获胜。这个交叉对比的过程也是个排列的问题,田忌这边有6种顺序,而齐王也是6种顺序,所以一共的可能性是6x6=36种。
我用代码模拟了一下,你可以看看。
public static void main(String[] args) {
ArrayList<String> t_horses = new ArrayList<String>(Arrays.asList("t1", "t2", "t3"));
Lesson7_2.permutate(t_horses, new ArrayList<String>(), t_results);
ArrayList<String> q_horses = new ArrayList<String>(Arrays.asList("q1", "q2", "q3"));
Lesson7_2.permutate(q_horses, new ArrayList<String>(), q_results);
System.out.println(t_results);
System.out.println(q_results);
System.out.println();
for (int i = 0; i < t_results.size(); i++) {
for (int j = 0; j < q_results.size(); j++) {
Lesson7_2.compare(t_results.get(i), q_results.get(j));
}
}
}
由于交叉对比时只需要选择2个元素,分别是田忌的出战顺序和齐王的出战顺序,所以这里使用2层循环的嵌套来实现。从最后的结果可以看出,田忌获胜的概率仍然是1/6。
暴力破解密码如何使用排列思想?
聊了这么多,相信你对排列有了更多了解。在概率中,排列有很大的作用,因为排列会帮助我们列举出随机变量取值的所有可能性,用于生成这个变量的概率分布,之后在概率统计篇我还会具体介绍。此外,排列在计算机领域中有着很多应用场景。我这里讲讲最常见的密码的暴力破解。
我们先来看去年网络安全界的两件大事。第一件发生在2017年5月,新型“蠕虫”式勒索病毒WannaCry爆发。当时这个病毒蔓延得非常迅速,电脑被感染后,其中的文件会被加密锁住,黑客以此会向用户勒索比特币。第二件和美国的信用评级公司Equifax有关。仅在2017年内,这个公司就被黑客盗取了大约1.46亿用户的数据。
看样子,黑客攻击的方式多种多样,手段也高明了很多,但是窃取系统密码仍然是最常用的攻击方式。有时候,黑客们并不需要真的拿到你的密码,而是通过“猜”,也就是列举各种可能的密码,然后逐个地去尝试密码的正确性。如果某个尝试的密码正好和原先管理员设置的一样,那么系统就被破解了。这就是我们常说的暴力破解法。
我们可以假设一个密码是由英文字母组成的,那么每位密码有52种选择,也就是大小写字母加在一起的数量。那么,生成m位密码的可能性就是52^m种。也就是说,从n(这里n为52)个元素取出m(0≤n)个元素的可重复全排列,总数量为n^m。如果你遍历并尝试所有的可能性,就能破解密码了。
不过,即使存在这种暴力法,你也不用担心自己的密码很容易被人破解。我们平时需要使用密码登录的网站或者移动端App程序,基本上都限定了一定时间内尝试密码的次数,例如1天之内只能尝试5次等等。这些次数一定远远小于密码排列的可能性。
这也是为什么有些网站或App需要你一定使用多种类型的字符来创建密码,比如字母加数字加特殊符号。因为类型越多,n^m中的n越大,可能性就越多。如果使用英文字母的4位密码,就有52^4=7311616种,超过了700万种。如果我们在密码中再加入0~9这10个阿拉伯数字,那么可能性就是62^4=14776336种,超过了1400万。
同理,我们也可以增加密码长度,也就是用n^m中的m来实现这一点。如果在英文和阿拉伯数字的基础上,我们把密码的长度增加到6位,那么就是62^6=56800235584种,已经超过了568亿了!这还没有考虑键盘上的各种特殊符号。有人估算了一下,如果用上全部256个ASCII码字符,设置长度为8的密码,那么一般的黑客需要10年左右的时间才能暴力破解这种密码。
小结
排列可以帮助我们生成很多可能性。由于这种特性,排列最多的用途就是穷举法,也就是,列出所有可能的情况,一个一个验证,然后看每种情况是否符合条件的解。
古代的孙膑利用排列的思想,穷举了田忌马匹的各种出战顺序,然后获得了战胜齐王的策略。现代的黑客,通过排列的方法,穷举了各种可能的密码,试图破坏系统的安全性。如果你所面临的问题,它的答案也是各种元素所组成的排列,那么你就可以考虑,有没有可能排列出所有的可能性,然后通过穷举的方式来获得最终的解。
思考题
假设有一个4位字母密码,每位密码是a~e之间的小写字母。你能否编写一段代码,来暴力破解该密码?(提示:根据可重复排列的规律,生成所有可能的4位密码。)
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。