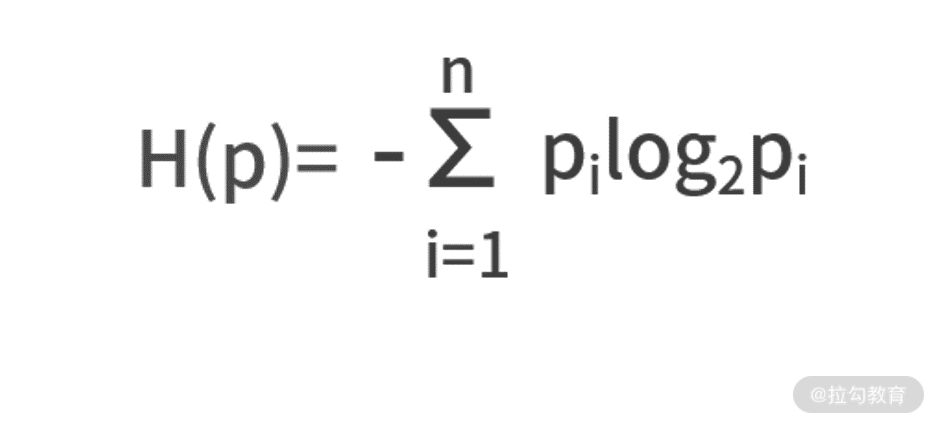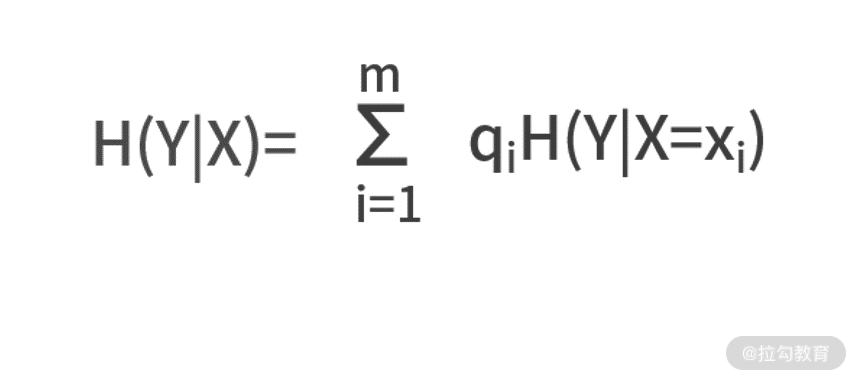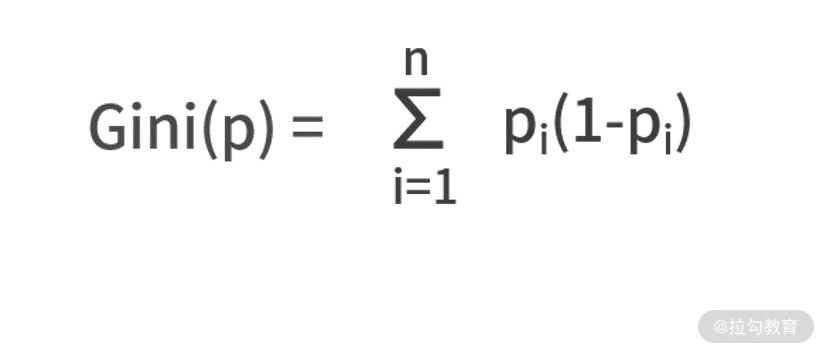10 信息熵:事件的不确定性如何计算?
你好,欢迎来到第 10 课时——信息熵:事件的不确定性如何计算?
从加乘法则开始,我们基于事情的不确定性出发,尝试计算事情发生的可能性。然而,对于事件与事件之间的不确定性如何相比和衡量,单独靠概率就无法说清楚了。我说的这句话是什么意思呢?下面我举个例子来说明。
假设有两场足球赛,也就是两个事件。第一场足球赛,对阵的双方是老挝队和巴西队,标记为事件 A;第二场足球赛,对阵的双方是阿根廷队和葡萄牙队,标记为事件 B。显然,在比赛开始前,这两个事件的比赛结果都具备一定的不确定性。人们也会根据历史数据,分别计算两场足球赛结果的概率。
现在我们思考这样的问题:事件 A 和事件 B 的比赛结果,哪个不确定性更大?
显然是事件 B。因为对于事件 A,除非爆冷,否则巴西队几乎是不可能输给老挝队的,事件 A 比赛结果的不确定性就很低;对于事件 B,阿根廷有梅西,葡萄牙有 C 罗,二者都是球星云集的老牌劲旅,比赛结果的不确定性就非常强。
所以这一讲,我们就来学习如何用一些量化的指标衡量事物的不确定性。
熵
事物的不确定性用“熵”表示。熵越大,则不确定性越强;熵越小,不确定性越小。熵的单位为 bit,所以熵的另一种理解是信息量。
那么什么样的事情的信息量更大呢?一定是对于不确定性事件的结果的信息。
例如,大迷糊向你说,“巴西队 vs 老挝队”的结果是巴西队获胜了,这句话对你而言就是废话,信息量非常少。相反,如果大聪明跟你说,“阿根廷 vs 葡萄牙”的比赛中葡萄牙获胜了,这句话对一个不确定性很强的事件给出了结果,其信息量就很大。
直观来说,越是“废话”,信息量越少;越是描述人们看不明白的事情,信息量就越大。
既然熵可以描述不确定性,那么具体到某个事件身上,熵应该怎么计算呢?我们给出熵的定义式。假设一个事件 A 有 N 个结果,每个结果发生的概率为 pi,那么熵的计算公式为:
我们给一个计算的例子。假设在“巴西队 vs 老挝队”的比赛中,巴西获胜的概率为 0.9,巴西队不胜的概率为 0.1,计算这场比赛的熵。根据定义式计算,可以得出 H(p) = -0.9 * log2 0.9 - 0.1 * log2 0.1 =0.4690。
对于熵的计算,涉及取对数的计算,我们给出下面的代码。
import math
def entropy(*c):
result = 0
islegal = 0
for x in c:
islegal += x
result = result + (-x) * math.log(x,2)
if islegal != 1:
return 'input prob error!'
return result
if __name__ == '__main__':
print entropy(0.9,0.1)
我们对代码进行解读。
- 从第 6 行开始,对输入的每个概率值进行循环。
- 每次循环的动作是,第 7 行计算概率的求和,并用 islegal 变量保存。
- 第 8 行,根据公式来计算熵的值,用 result 变量来保存。
- 最终,判断概率之和是否为 1,如果不是,则输出错误信息;如果没问题,则返回 result。
以上代码执行的结果如下图所示:
接下来,我们换一个事件计算。假设对于“阿根廷 vs 葡萄牙”的比赛中,阿根廷获胜的概率为 0.4,阿根廷不胜的概率为 0.6,试着再来计算下熵的值。
这次,我们直接用代码来运算。将第 15 行,更改为 print entropy(0.4,0.6),运行结果如下图所示:
可见,此时的熵值比之前“巴西队 vs 老挝队”的要大,因此“阿根廷 vs 葡萄牙”比赛结果的不确定性更强、信息量更大。
条件熵
在概率的学习中,我们学过概率和条件概率。对于熵而言,也有对应的条件熵。条件熵衡量的是,在某个条件 X 下,事件 Y 的不确定性是多少,记作 H(Y|X)。
假设,条件 X 有 m 个可能结果,每个结果发生的概率为 qi,则条件熵的定义式为:
其中 H(Y|X=xi)表示在某个 xi 条件下 Y 的熵。
这个公式有点复杂,我们继续以足球赛的结果为例去理解公式。
假设“巴西队 vs 老挝队”的足球比赛中,正常情况下巴西队获胜的概率为 0.9。然而,最近巴西的天气不太好,球员受到天气的影响后,患病的概率非常高。假设每个球员患病的概率都是 0.5。而且一旦球员患病,巴西队获胜概率将降低到 0.6。那么,我们试着去计算球员身体状况为条件的比赛结果的熵。
我们套用上面的公式来进行计算。标记事件 Y 为比赛结果,条件 X 为球员是否健康。根据例子的信息,X 有两个可能性,分别是 x1(健康)和 x2(患病),且两个可能性发生的概率为 q1= q2= 0.5。
接着,先需要分别计算每个条件下的熵H(Y|X=xi):
- 健康的情况下,H(Y|X=x1) =-0.9×log20.9-0.1×log20.1 = 0.4690;
- 患病的情况下,H(Y|X=x2) =-0.6×log20.6-0.4×log20.4 = 0.9710。
因此,球员身体状况为条件的比赛结果的熵为H(Y|X) = q1*H(Y|X=x1)+ q2*H(Y|X=x2) = 0.5 * 0.4690 + 0.5 * 0.9710 = 0.72。
信息增益可以描述条件熵和熵的关系
“熵”的含义是不确定性,而“条件熵”的含义是知道了某个条件下的不确定性。因此直觉来看,条件熵应该小于或等于熵,因为增加了“某个条件”就等于是知道了某个信息,最不济就是个无用信息,但无论如何一定会让“不确定性”减小。
这个结论的证明会很复杂,感兴趣的同学可以自己试着推导下。我们借助刚刚的足球比赛的例子,来验证这个结论。先通过这个表格,利用“08 | 加乘法则:如何计算复杂事件发生的概率?”中的加乘法则,分别计算出巴西队获胜和不胜的概率: 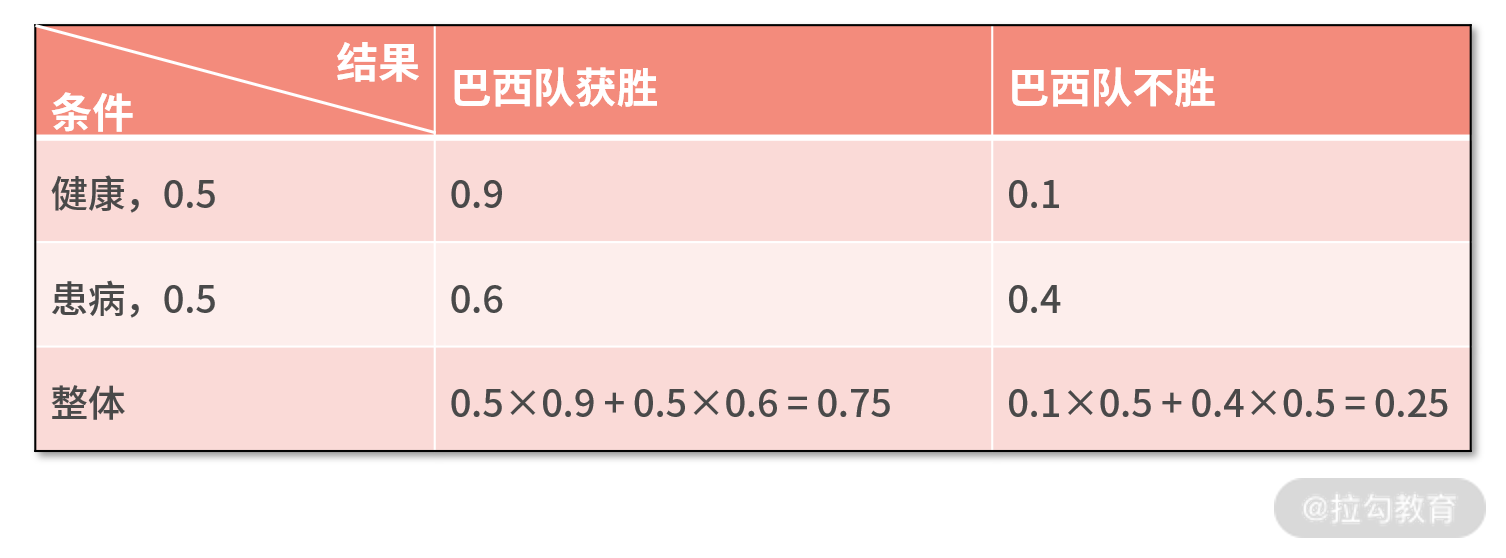

- 信息增益,顾名思义就是信息量增加了多少;换句话说,也是不确定性降低了多少。标记为 g(X,Y),定义式为 g(X,Y) = H(Y) - H(Y|X)。
- 有时候,除了看这个差值以外,还会同时观察降幅的比值。此时为信息增益率,定义式为 gr(X,Y) = g(X,Y) / H(Y)。
回到刚刚足球比赛的例子,它的信息增益为 g(X,Y) = H(Y) - H(Y|X) = 0.8113 - 0.7200 = 0.0913;信息增益率为 gr(X,Y) = g(X,Y) / H(Y) = 0.0913 / 0.8113 = 11.25%
基尼系数
最后,我们再介绍一个描述事物不确定性的方法——基尼系数,标记为 Gini(p)。
这里的基尼系数与衡量国民收入差距的基尼系数是不同的概念,所以不必纠结两者的区别。
基尼系数和熵一样,都是在描述信息量,区别在于二者的计算定义式不同。相对于熵的定义式,基尼系数的定义式只是把其中的 -log2pi替换为(1-pi),则有
我们仍然围绕“巴西队 vs 老挝队”“阿根廷队 vs 葡萄牙队”的比赛,来计算一下基尼系数。
- 对于巴西队的比赛而言,其基尼系数为 Gini(p) = 0.9(1-0.9) + 0.1(1-0.1) = 0.18
- 对于阿根廷对的比赛而言,其基尼系数为 Gini(p) = 0.4(1-0.4) + 0.6(1-0.6) = 0.48
显然,阿根廷队的比赛基尼系数更大,不确定性更强。定性的结果与熵的计算方式是一致的。
利用“信息增益”制定计划
讲了这么多不确定性的计算方法,那么它们到底有什么实际应用的场景呢?其实,描绘出事物的不确定性,更多的是帮助人们做出正确的选择。
我们说过,熵的由高到低,就是信息量的由高到低,也就是不确定性的由高到低。也就是,熵越低的事情,越接近废话,也就越有把握。那么我们在调节资源投入的时候,就应该尽量避免在熵低的事情上的投入;相反,应该投入到熵比较高的事情上。
所以,当明确了要在熵高的事情上投入资源后,就要想办法让这个事情的熵逐步降低,让它的不确定性降低,你可以理解为解决问题的过程就是让熵减少的过程。而要让熵减少,就需要不断地有外部条件输入。通过外部条件输入,获得信息增益,来不断降低熵。
上面的描述很抽象,我们用一个具体的例子来说明,假设大漂亮是某公司的总监。在下个月,有两个同等重要的技术方向,分别标记为 A 和 B。按照现在的发展趋势来看,A 方向在下个月成功解决的概率为 0.9,无法解决的概率为 0.1;B 方向在下个月成功解决的概率为 0.6,无法解决的概率为 0.4。
此时就如同刚刚的足球赛一样。A 的熵为0.4690,B 的熵为 0.9710。显然,B 的不确定性更强,是更需要投入人力去解决的。因此大漂亮决定把资源向 B 倾斜,安排了两名工程师去解决 A 问题,而安排了 5 名工程师去解决 B 问题。
接着,大漂亮仍然感觉 B 方向的不确定性很强,怎么办呢?她想到,要通过引入外部条件,来降低 B 的熵。因此她通过社招,招聘到了一名 B 技术方向的资深专家大聪明。大聪明的加入,显然是个外部条件,带来了信息增益;因此,B 技术方向的不确定性就在下降。最终在月底,A 方向和 B 方向,都取得了技术突破。
小结
我们再回顾一下“概率”和“熵”的区别。对于一个事件而言,它可能有很多个结果。例如,“老挝队和巴西队的足球比赛”这是一个事件,而这个事件有很多可能的结果,例如巴西队胜、巴西队不胜。
- 概率,描述的是某个事件的结果,发生的可能性。有时候,在不刻意强调区分“事件”和“事件结果”的时候,也被简称为事件发生的可能性。
- 熵,描述的则是事件背后蕴含的信息量和不确定性。
你也可以理解为,“可能性”探讨的是事件某个结果的发生;而“不确定性”探讨的是一个事情下的不同结果发生的情况。
最后总结一下这一讲的要点。熵是描述事物不确定性的量。在定量描述了事物的不确定性之后,可以辅助人们做出更加合理的资源分配决策。条件熵,是指引入了某个外部条件后的熵;条件引入,必然会带来信息增益,也就是会让熵变小,这个变小的幅度可以用信息增益或信息增益率来描述。
这四个关键概念的定义式如下,你可以通过定义式去反复领悟它们之间的区别和意义。