20 算法思想:JS中分治、贪心、回溯和动态规划
你好,我是石川。
在算法中,我们提到如递归、分治、贪心、回溯和动态规划这些不同的算法思想时一般会分开来说。但实际上,它们之间是有着关联的。比如递归和回溯可以解决贪心顾及不到或者不能重试的问题。而动态规划又可以在利用递推公式的基础上解决递归中的一些短板。
能够比较好贯穿整个思想的是一个硬币找零的例子,即在几种不同面值硬币中,如何用最少的硬币数量来找零的问题。
贪心和递归分治
首先,我们来看下贪心算法如何解这个题。找零问题的核心是在几种不同面值如1、5、10分的硬币中,用最少的枚数凑出针一个需要找零的钱数。解决这个问题最简单的办法就是使用贪心(greedy)算法,它的核心逻辑是我们先选择面值较大的来找,再逐渐选小面额的。为什么这里是从大到小,而不是从小到大呢?因为通常面值越大,用到的数量就越少。
function minCoinChange(coins, amount) {
var change = [];
var total = 0;
for (let i = coins.length; i >= 0; i--) { // 从大到小循环
var coin = coins[i];
while (total + coin <= amount) { // 将硬币逐个加入,面值要小于商品价格
change.push(coin); // 将硬币加入到结果
total += coin; // 将硬币累加到总数
}
}
return change;
}
贪心是最简单的一种解决方案,可是这种方案有两个核心问题:
- 这种方式有时是得不到答案的,比如我们要找的钱数是17元,此时有面值为3元和5元的硬币。我们用了三张5元的后,还差2元要找,可这时我们只有3元,就没法找了。但如果我们先用3元,可以用四张3元加一张5元,就能得到17元。
- 这种方式得到的答案不一定是最优解。比如我们有面值为1、3、4元的硬币,需要找6元。如果先用4元,就要再加两张1元,这时硬币数一共三张。如果用3元的,只需要两张即可。
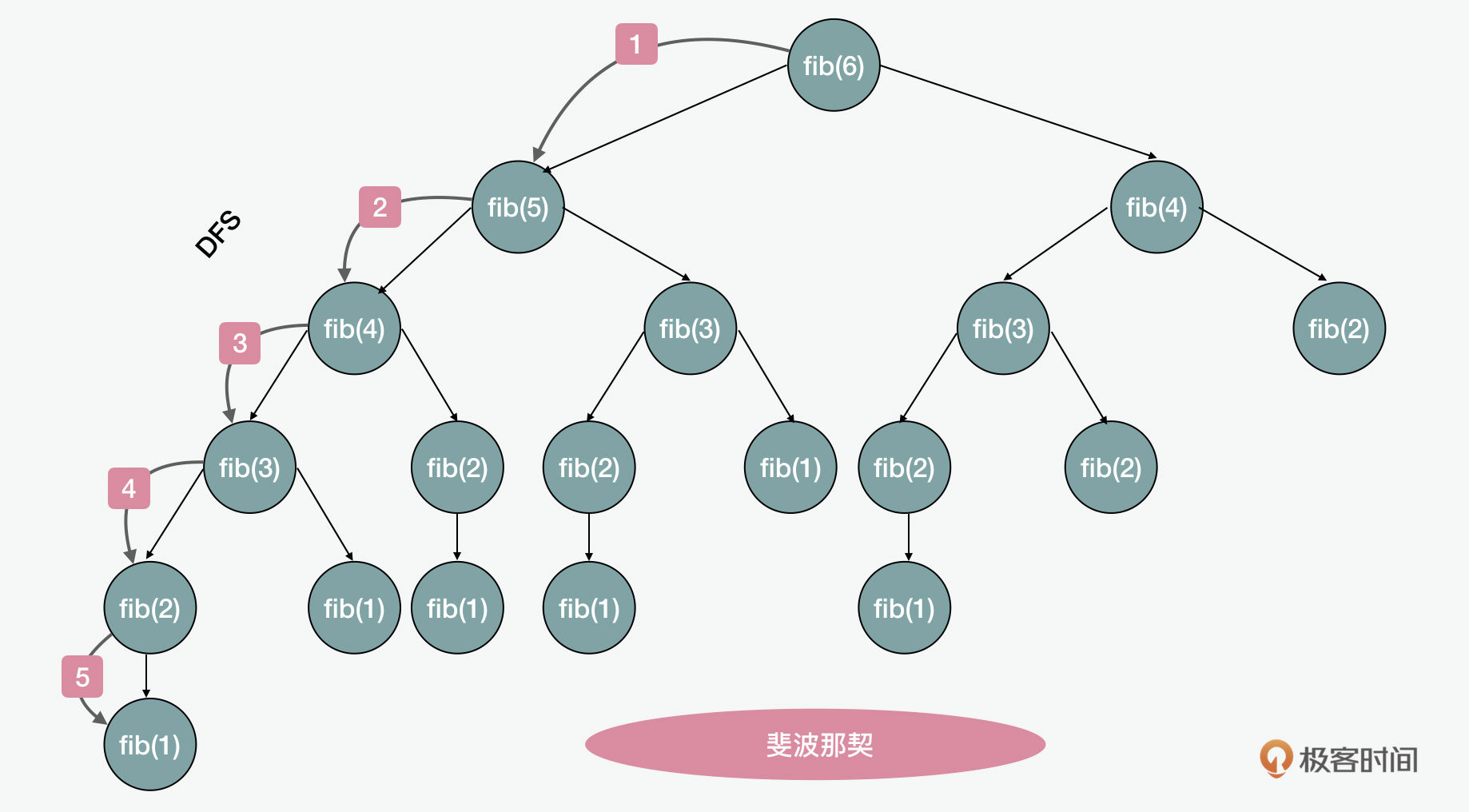
所以从运用贪心算法的例子里,我们可以看到,在有些情况下通过贪心算法可以得到局部最优解,可是没法保证全局的最优解,甚至有些时候都没有解。那么有什么更好的方式可以做到找零呢?另一种方式就是用到递归(recursion) 和 分治(divide and conquer) 了。我们先回到之前说过的斐波那契数列。我们看,用递归的方式来求解斐波那契中的例子,这个过程像什么呢?没错,它像是我们上一讲说到的树(tree) 形的数据结构,而且它的遍历过程就如同是一个深度优先(DFS)的遍历顺序。
回溯和记忆函数
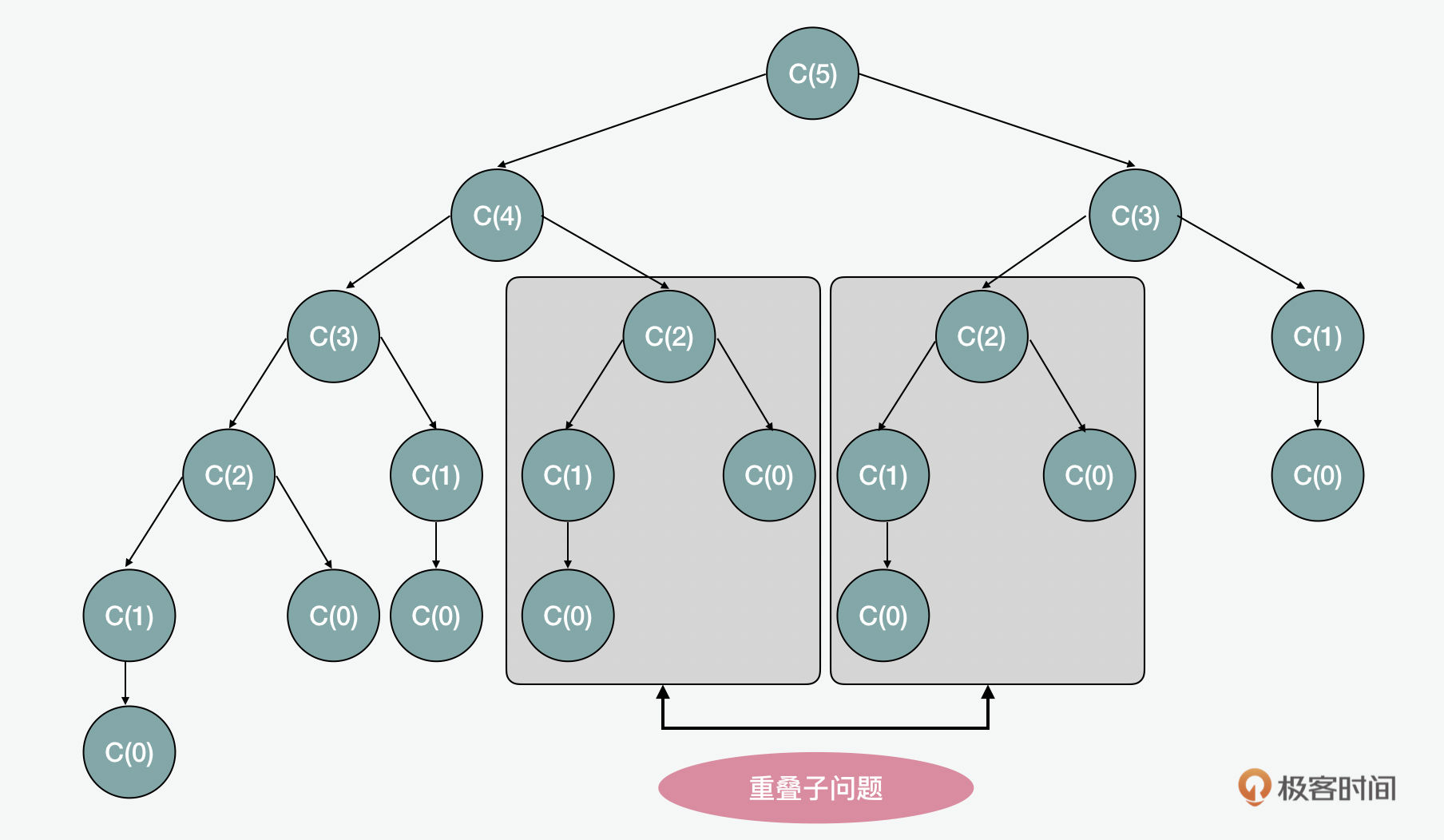
而我们所说的硬币找零的例子,和斐波那契相似,它也可以通过这样类似的一棵树来求解。这里我们也可以使用暴力递归的算法。这样,我们可以看到通过暴力枚举的朴素方式,就可以解决贪心带来的问题。但是这样也会带来新的问题,就是重叠子问题(overlapping subproblems)。假设我们有一个5元的商品,和面值为1和2的硬币。那么在找零的过程中,我们可以看到很多的重复计算。这个问题也很像我们之前在解斐波那契时遇到的去重问题。
那我们如何解决重叠子问题呢?拿找零的场景举例,我们可以将贪心和递归结合,通过减枝的方式来优化递归算法。前面我们说过贪心的核心问题之一是没办法回溯,而我们之前在讲到递归的时候,讲到过基于堆栈和栈帧的原理,先从贪心的方法开始尝试,如果成功,就继续执行。如果不成功,就回到上一步,换一种方法执行,这样就解决了类似的问题。而这里面,就用到了回溯(backtracking) 的思想。同样的,我们也可以通过记忆函数创建一个备忘录(memoization),来起到在执行中去重的作用。
递推和动态规划
那如果从上面的例子来看,这和我们之前讲的递归就没有太大不同了。那还有没有解决这个问题更高效的方法呢?下面我们再来看看动态规划(dynamic programming)。这里有两个重要的概念,第一个是无后效性,第二个是最优子结构。后无效性是说,如我们上图中所示,一个顶点下的子问题分支上的问题之间,依赖是单向的,后续的决策不会影响之前某个阶段的状态。而最优子结构指的是子问题之间是相互独立的,我们完全可以只基于子问题路径前面的状态推导出来,而不受其它路径状态的影响。这就好比我们在点外卖时,如果两个商品同时有优惠,那么要达到最大的优惠额度,我们就直接买两个打折后的商品就好了。但是假如折扣只能用于同一订单中的一个产品,那么我们可能就要选单价最高的商品打折。这时,我们的一个分支的选择会影响另外一个分支的选择,这种情况就不能算是最优子结构了。
我们看在找零问题中,没有以上影响。所以我们可以考虑动态优化。在动态规划中,解决问题用的是状态转移方程,其中包含了几个核心的元素,第一个就是初始化状态,它虽然叫初始状态,其实代表的是终止状态。在找零的例子里,我们希望最后找零的结果是0,所以,初始状态就是0。第二个核心元素就是状态参数,它指的是剩下需要找的零钱。我们每次在找零的过程中,就是这个状态在不断消减的过程,也就是最后它应该归零,达到初始状态。在上面的决策树中,我们看到每次选择的过程中,我们都要在一组集合中选中一种面值的硬币,这种选择,就是决策。
对于找零来说,我们可以写出状态转移方程$\(min(DP\[i\], DP(i-coin)+1)\)\(它的思考模式就是我们之前讲递归的一讲中提到**递推公式**时的思考模式,也就是说,我们自底而上的思考,如果我们决定用一枚硬币,那么就要加\)DP(i-coin)+1\(。如果我们不采用,那就是\)DP[i]\(。因为这是一个求最值的问题,所以我们通过\)min()$来对比两种决策中最小的值。
这时,你可能会有一个疑问,如果状态转移方程就是个递推公式,那为啥我们不直接用递归呢?动态规划和它有啥区别?这是因为如我们之前所讲,递归的特点是一递一归,先自上而下深度优先遍历的,这个过程是基于堆栈的原理实现的,就会产生额外的花费。而且从上到下的过程中,不能完全避免冗余的分支计算。所以为了解决这个问题,动态规划就派上用场了。它是通过两层嵌套的迭代循环,在内循环中,用到转移方程,自下而上的计算,解决了不必要的时间消耗。这样看,它可能不是那么函数式(声明式),而更命令式,但是它确实在执行效率上会更高。
function minCoinChange(coins, amount) {
var dp = Array(amount + 1).fill(Infinity); // 每种硬币需要多少
dp[0] = 0; // 找0元,需要0个硬币
for (let coin of coins) { // 循环每种硬币
for (let i = coin; i <= amount; i++) { // 遍历所有数量
dp[i] = Math.min(dp[i], dp[i - coin] + 1); // 更新最少需要用到的面值
}
}
return dp[amount] === Infinity ? -1 : dp[amount]; // 如果最后一个是无限的,没法找
}
所以如果我们追求的是效率的话,那么动态规划在这个例子中是最高的。
延伸:位运算符
讲完以上几种算法,我还想再延伸一点知识。在数据结构和算法中,除了动态规划外,还有哪些可以提高性能的算法思想呢?这里我们可以结合JavaScript的特性看看位运算(bitwise operation)的使用和思想。
在JavaScript中,整数都是32位的由0和1表示的二进制比特序列。举个例子,在位运算中,101就代表5可以用101来表示,9可以用1001来表示。
按位与(& AND)表示的是,对于每一个比特位,如果两个操作数相应的比特位都是1时,结果则为1,否则为0。 比如5&9的运算结果就是0001,也就是1。
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 // 5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 // 9
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 // 5&9
那么以此类推,对于按位或(I OR)来说,针对每一个比特位,当两个操作数相应的比特位至少有一个1时,结果为1,否则为0。比如 5|9的运算结果就是1 1 0 1,也就是13。
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 // 5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 // 9
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 // 5|9
那么对于按位非(~ NOT)来说,指的则是反转操作数的比特位,即0变成1,1变成0。那么~5的运算结果就是-6,~9的运算结果就是-10。
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 // 5
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 // -5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 // 9
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 // -9
接下来我们再看看按位异或(^ XOR),它的操作是对于每一个比特位,当两个操作数相应的比特位有且只有一个1时,结果为1,否则为0。那么5^9的运算结果就是1 1 0 0,也就是12。
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 // 5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 // 9
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 // 5^9
下面我们再来看看位移。这里又分为左移(<< Left shift),有符号右移(>> Right shift)和无符号右移(>>> Zero-fill right shift)。左移会将 a 的二进制形式向左移 b (< 32) 比特位,右边用0填充,所以9<<1的结果就是18。而有符号右移则会将 a 的二进制表示向右移 b (< 32) 位,丢弃被移出的位,所以9>>1的结果就是4。最后无符号右移会将 a 的二进制表示向右移 b (< 32) 位,丢弃被移出的位,并使用 0 在左侧填充,所以9>>1的结果就是2147483643。
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 // 9
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 // 9 << 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 // 9 >> 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 // 9 >>> 1
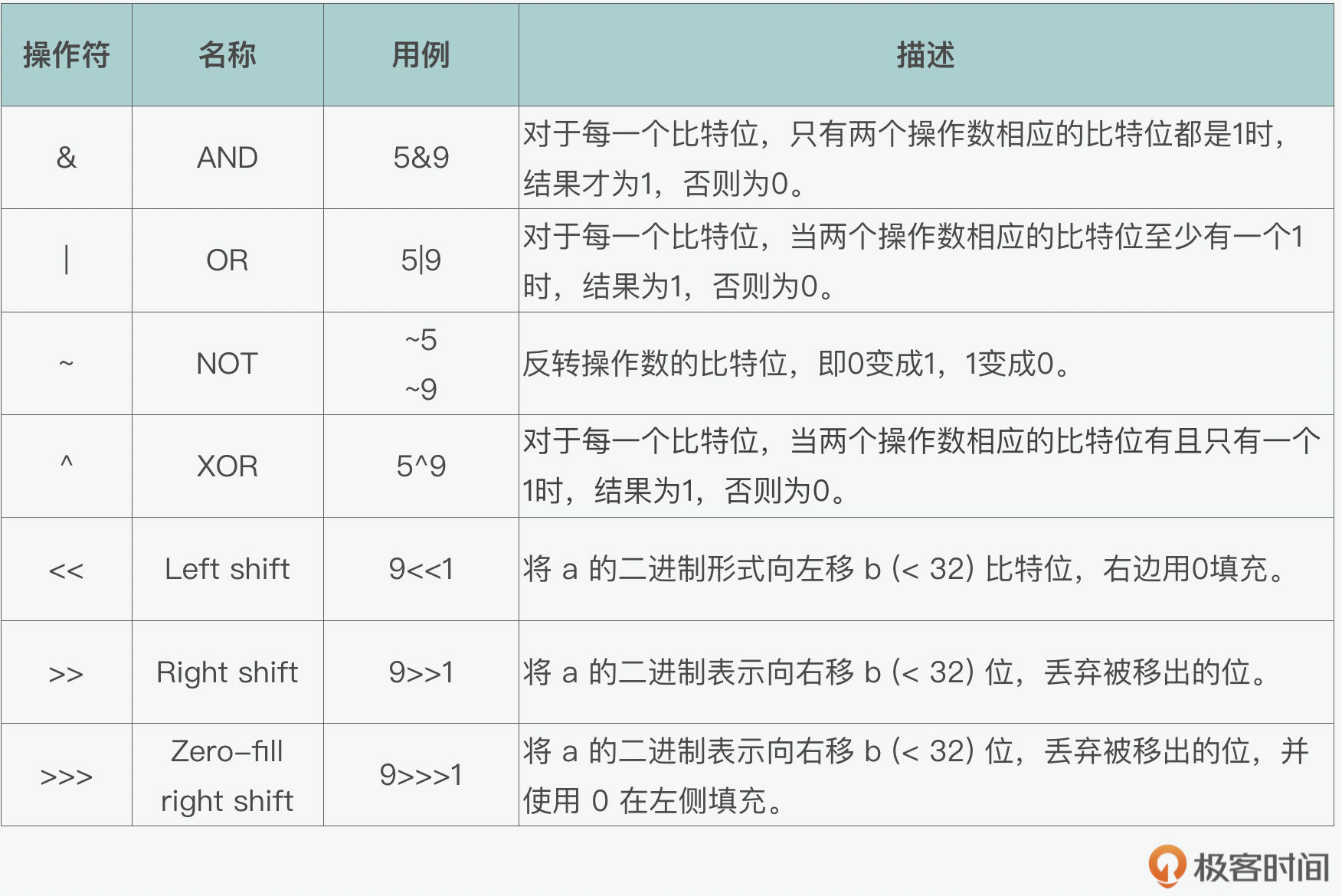
我们可以用一个列表来总结下相关的操作符,这样看起来更直观。
那么学会了位运算后,我们的加减乘除都可以通过位运算来计算。比如加法计算就可以用位运算来进行,这和我们小学时学的数学是一样的,我们在学10进制的加法时,就是在遇到10的时候,进一位。同样的方式,也可以用于位运算。这里同样可以用到递归或循环。下面,你可以参考一个递归的例子。
var add = function(a, b) {
if (b == 0) {
return a;
} else {
return add(a ^ b, (a & b) << 1);
}
};
位运算从一定程度上可以让计算的效率更高,但是这样也会牺牲一定的可读性。所以在使用上,应该综合考虑。
总结
这节课就到这里,最后我来做个小结。今天,我们看到了算法中的贪心、递归、分治、回溯和动态规划并不是完全独立的,它们在某种意义上是相连的。其实算法思想不光是用在程序中,如果我们仔细观察不同行业很成功的人和团队,多多少少都能发现他们具有算法思想。比如在当年解放战争时期,为什么解放军能赢,就是用到了类似分治和动态规划的思想。看似以少胜多,但每次通过分治,可以在局部以多胜少。同时通过动态规划防止局部成功来带的贪心思想,而是时刻关注着全局最优解,最后取得了全面的胜利。所以通过JS的原理,学好算法,不仅仅是纸上谈兵,而是可以在工作和生活的方方面面帮助我们“运筹帷幄之中,决胜千里之外”。
思考题
今天的思考题是,关于找零的问题,除了贪心和动态规划的实现,你能不能也用文中提到的递归和回溯来动手实现下找零。
期待在留言区看到你的分享,我们一起交流讨论。另外,也欢迎你把今天的内容分享给更多的朋友。我们下期再见!